Research

Research interests

I am working towards formalizing results about \(Out(F_n)\), with the specific goal of eventually formalizing the proof of the existence and uniqueness of greedy folding paths (due to Bestvina). This is the Outer Space analog of Teichmüller's existence and uniqueness theorem.

In graduate school, my research focused on the dynamics of the mapping class group action on Teichmüller space, and specifically the action of the mapping class groups of non-orientable surfaces. Mapping class groups of non-orientable surfaces have surprisingly different dynamics compared to their orientable counterparts. The dynamics is not so well behaved, and the geodesic flow on the quotient is not recurrent for almost every orbit, with respect to the natual measure. My work focused on understanding the poor behavior, as well as building better measures with respect to which the geodesic flow is better behaved. This has applications in counting simple closed curves on non-orientable surfaces: for orientable surfaces, the simple closed curve counting was solved by Mirzakhani using dynamical techniques as well.

Papers

1. (PhD thesis) Dynamics on the Moduli Space of Non-Orientable Surfaces. (Link to UMich thesis repository) (abstract)
   The moduli spaces of non-orientable hyperbolic surfaces have conjectural similarities to infinite volume geometrically finite hyperbolic manifolds. This thesis establishes some of the conjectured analogies to geometrically finite hyperbolic manifolds, which are useful in the context of understanding the geodesic flow on the unit cotangent bundle of the moduli space. In particular, it is shown that the Patterson-Sullivan measure is supported on the set of projective measured foliations containing no one-sided leaves. We then also show that the action of the mapping class group on the Teichmüller space, restricted to a finite covolume subset, is statistically convex-cocompact. We deduce from this that the Patterson-Sullivan measure is non-atomic, and the Bowen-Margulis measure on the unit cotangent bundle is finite, and the geodesic flow is ergodic with respect to this measure.
   
2. Statistical convex-cocompactness for mapping class groups of non-orientable surfaces. (arXiv:2404.11293) (abstract)
   We show that a finite volume deformation retract 𝒯_εt⁻(𝒩_g)/MCG(𝒩_g) of the moduli space of non-orientable surface ℳ(𝒩_g) behaves like the convex core of ℳ(𝒩_g), despite not even being quasi-convex. Moreover, we show that geodesics in the convex core leave compact regions with exponentially low probabilities, showing that the action of MCG(𝒩_g) on 𝒯_εt⁻(𝒩_g)/MCG(𝒩_g) is statistically convex-cocompact. Combined with results of Coulon and Yang, this shows that the growth rate of orbit points under the mapping class group action is purely exponential, pseudo-Anosov elements in mapping class groups of non-orientable surfaces are exponentially generic, and the action of mapping class group on the limit set in the horofunction boundary is ergodic with respect to the Patterson-Sullivan measure. A key step of our proof relies on complexity length, developed by Dowdall and Masur, which is an alternative notion of distance on Teichmüller space that accounts for geodesics that spend a considerable fraction of their time in the thin part.
   
3. The limit set of non-orientable mapping class groups. (In Journal of Modern Dynamics; arXiv:2110.00037) (abstract)
   We provide evidence both for and against a conjectural analogy between geometrically finite infinite covolume Fuchsian groups and the mapping class group of compact non-orientable surfaces. In the positive direction, we show the complement of the limit set is open and dense. Moreover, we show that the limit set of the mapping class group contains the set of uniquely ergodic foliations and is contained in the set of all projective measured foliations not containing any one-sided leaves, establishing large parts of a conjecture of Gendulphe. In the negative direction, we show that a conjectured convex core is not even quasi-convex, in contrast with the geometrically finite setting.
   
4. Pseudo-Anosov homeomorphisms of punctured non-orientable surfaces with small stretch factor. With Caleb Partin and Becca Winarski. (In Algebraic & Geometric Topology; arXiv:2107.04068) (abstract)
   We prove that in the non-orientable setting, the minimal stretch factor of a pseudo-Anosov homeomorphism of a surface of genus g with a fixed number of punctures is asymptotically on the order of 1/g. Our result adapts the work of Yazdi to non-orientable surfaces. We include the details of Thurston's theory of fibered faces for non-orientable 3-manifolds.
   

Computer experiments

I also write computer programs to assist in visualization of exotic geometric objects, as well as testing small conjectures. I usually upload my cleaned up code on Github, but if it's a small one-off program, I might not make it public. In case you would like access to the code anyways, let me know, and I will be happy to share it.

Limit set of a non-orientable mapping class group

A part of the limit set of the mapping class group of a non-orientable surface of genus 6 when restricted to a 3-dimensional stratum of projective measured foliations. Unlike in the orientable case, the limit set is not the entire stratum, but rather a nowhere dense measure 0 subset. The Hausdorff dimension of the limit set restricted to a dimension n-stratum is bounded between n-1 and n-2, where the upper bound is sharp. Locally, the limit set is contained in a hyperplane, and the image is a rendering of the limit set when restricted to one such hyperplane.

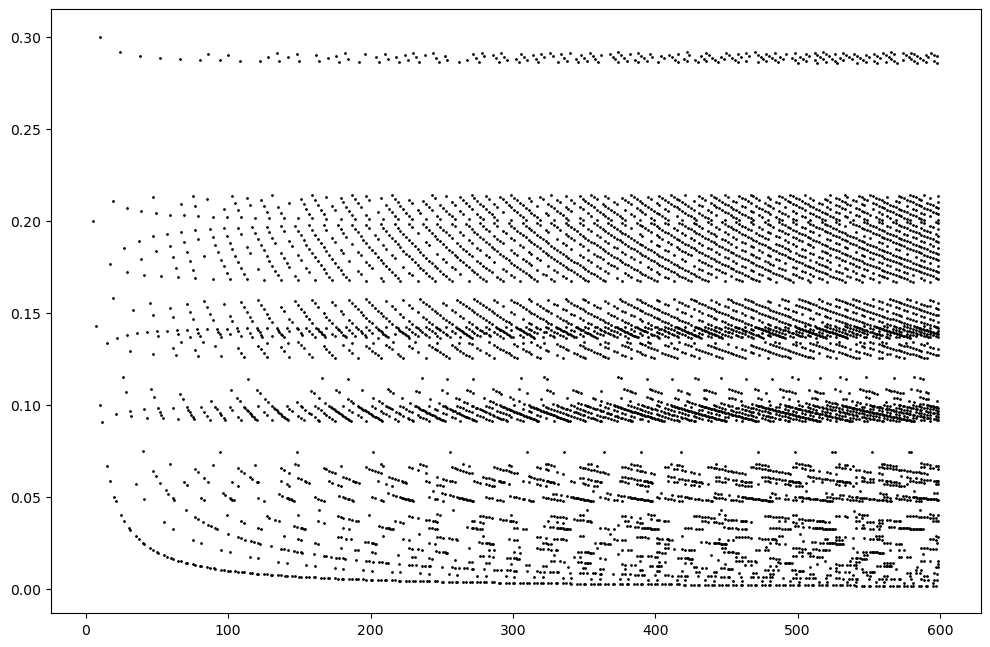
Resolving intersections of parallel copies of intersecting curves

Given two two-sided curves on a non-orientable surface with positive intersection, we can take m and n parallel copies of the curves and resolve all the intersections in a consistent manner to get a multicurve. This code resolves all the intersection, and counts the number of one-sided and two-sided components of the resulting multicurve. If there are no one-sided components, the program plots the point \((m+m, \frac{m}{m+n})\) on a scatter plot. The fact that the projection to the y-axis is not dense in \([0,1]\) seems to suggest that a convex combination of two minimal foliations that are approximable by two-sided multicurves may not itself be approximable by two-sided multicurves.